@marko_ribar wrote:
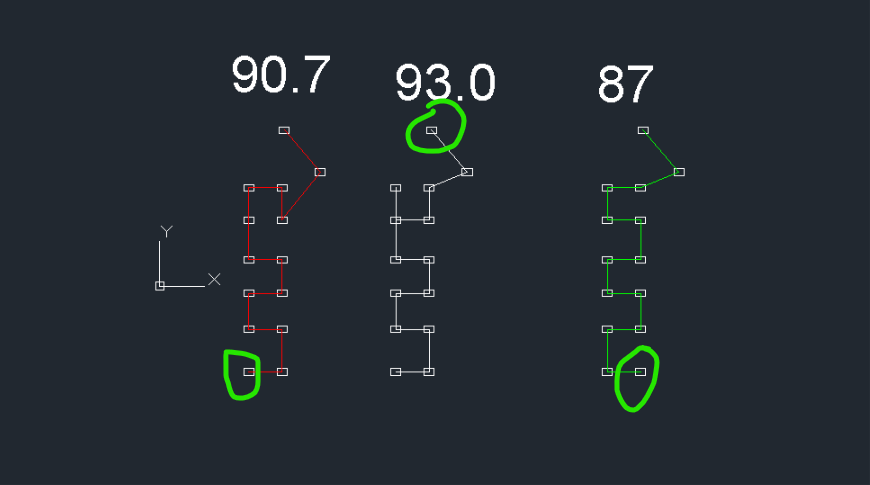
Both codes works the same way, and connect.lsp by me is faster than john's version... You added one imaginary point on your left example and starting point isn't the same... Sorry, but you haven't convinced me that your marked solution is correct... This is like I said just greedy algorithms attempts... Solution can't be found for more than 10 points... Real solution also should include beside checking for shortest overall distance intersections that may occur, like @dbhunia mentioned, and neither route.lsp nor connect.lsp check for this... Look in picture to see what I mean... You are cheating - see red circles...
You are right. I did not noticed that Route.lsp generated a point from the biggest circle. (because route.lisp just link circles)
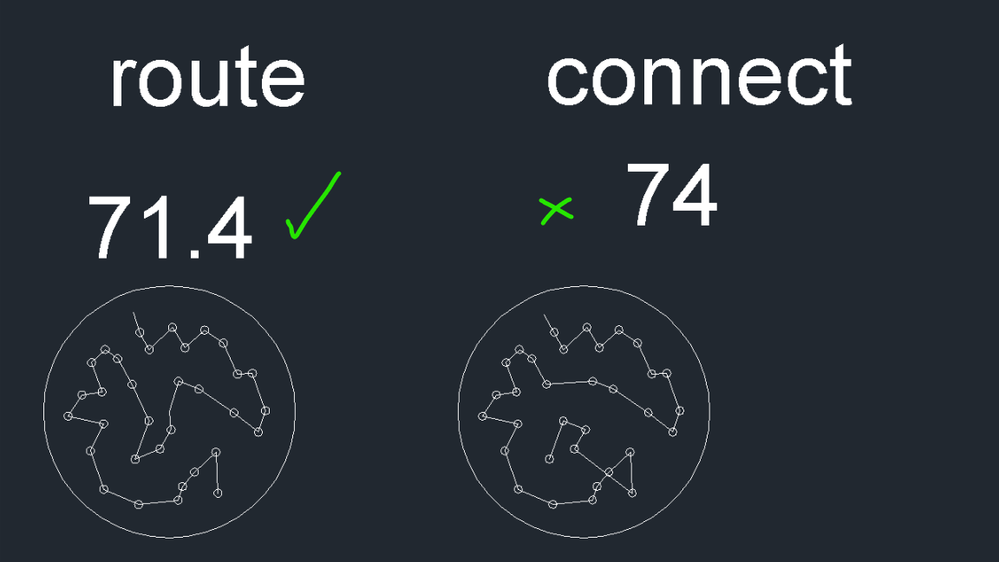
(file tested attached) In this image, I compared 3 lisp routines (route.lsp, connect_block.lsp attached named 'connect' in this image and connectblk.lsp attached and named 'connect-closed' in image). now and this is the result.

connect_block.lsp is the smallest length in this image. but connect_closed.lsp connect all points with a clear polyline. but routes did not the best here.
I already read that post from swamp.org, they are trying a mathematical solution, but in the real world does not have sense generate that unnecessary work for our CPU, because of obviously polylines that has the longest length always draw lines that going over other lines and vice versa.
I never thought to add an imaginary point to create the smallest line length. this is pretty interesting and is new for me. maybe creating an imaginary point might solve this issue.
EDIT: route.lsp and connect.lsp should have the same result. but I'm that test did not happen. I don't know what happened there.