How can I create dimension line that is not parallel to detail line

[Anonymous]

I am trying to create a dimension line that measures the z-component of a sloped detail line. I can do this in Revit but cannot figure out how to do it with the API. I've used Revit Lookup to compare the differences in the dimension lines. The ReferenceArray is the same but the main difference seems to be the Curve property which I'm assuming is set with the Line property when I call NewDimension(Section, Line, ReferenceArray). 

Here is my code:

            XYZ point3 = new XYZ(417.8, 80.228, 46.8);
            XYZ point4 = new XYZ(417.8, 80.811, 46.3);

            Line geomLine3 = Line.CreateBound(point3, point4);

            Plane geomPlane = new Plane(XYZ.BasisX, XYZ.Zero);
            using (Transaction tx = new Transaction(doc))
            {
                tx.Start("tx");
                SketchPlane sketch = SketchPlane.Create(doc, geomPlane);
                DetailLine line3 = doc.Create.NewDetailCurve(viewSection, geomLine3) as DetailLine;

                ReferenceArray refArray = new ReferenceArray();
                refArray.Append(line3.GeometryCurve.GetEndPointReference(0));
                refArray.Append(line3.GeometryCurve.GetEndPointReference(1));
                XYZ dimPoint1 = new XYZ(417.8, 80.118, 46.8);
                XYZ dimPoint2 = new XYZ(417.8, 80.118, 46.3);
                Line dimLine3 = Line.CreateBound(dimPoint1, dimPoint2);
                Dimension dim = doc.Create.NewDimension(viewSection, dimLine3, refArray);
                
                tx.Commit();
            }

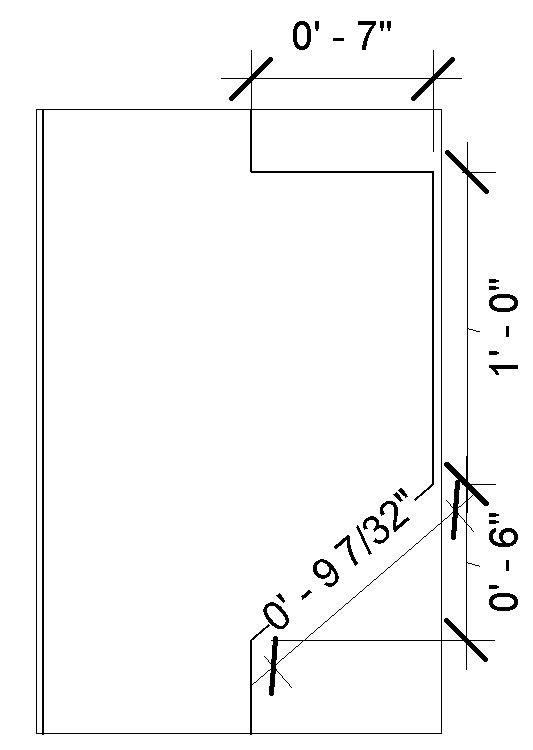
The line I'm sending into NewDimension is along the z-axis, but the dimension line I'm given is sloped parallel to the detail line and gives the length of the detail line when I want just the z-component. Using Revit Lookup I see the Curve Direction has a y- and z-component for Direction (0, 0.759, -0.651). When I create the line I want in Revit itself the Curve has a Direction of (0, 0, 1) and gives just the length of the z-component of the sloped detail line. 

Attached is an image of the section with the sloped detail line at the bottom right. It shows the dimension I create with the API (labeled with length of 0' - 9 7/32") and the one I create in Revit that I want to create with the API (labeled as 0' - 6").

 

Thank you for any help on this problem.

[jeremytammik]

Maybe you should snoop further. I the Z direction dimension in a different plane, on a different work plane, on a different sketch plane or something like that? I cannot imagine that you can create dimensions in all 3D space dimensions on the same plane. You need to switch the plane (some plane, no idea which) somehow. Don't you?

[Anonymous]

Jeremy,

Thank you for the response.

I think I'm in the correct plane. I'm in the Y-Z plane with the X-axis perpendicular to the plane and trying to measure a dimension in the Z-direction. This works with a detail line that has end points with the same Y-coordinate or same Z-coordinate, but is not working with the detail line with end points with different Y-coordinates and Z-coordinates, though X-coordinates are the same, so still in the Y-Z plane.

I did some more debugging in the code I posted earlier. I found that the Dimension object returned by doc.Create.NewDimension is correct and what I want. For example it has the value string of "0' - 6\"" which is the length of the detail line in the Z-direction as I expect. But after the call to Transaction.Commit() the Dimension object changes. For example the value string changes to "0' - 9 7/32\"" which is the total length of the detail line.

So the call to Transaction.Commit() is changing that Dimension object and forcing the dimension line to be parallel to the detail line. So I tried setting the Dimension property IsLocked to True before calling Commit() hoping that would fix the problem but does something even more odd. I'll attach an image to show the new output, which has a line with the correct value string but is parallel to the detail line instead of only in the z-direction.

Thank you for any help with this issue.

[jeremytammik]

Dear Frank,

Thank you for your update and further exploration.

That does sound very odd indeed.

Can you please provide a reproducible case for this that I can pass on to the development team?

http://thebuildingcoder.typepad.com/blog/about-the-author.html#1b

• A short exact description of what you are trying to achieve.
• The behaviour you observe versus what you expect, and why this is a problem.
• A complete yet minimal Revit sample model to run a test in.
• A complete yet minimal macro embedded in the sample model or Visual Studio solution with add-in manifest that can be compiled, loaded, run and debugged with a single click to analyse its behaviour live in the sample model.
• Detailed step-by-step instructions for reproducing the issue, e.g. which element to pick, what command to launch etc.

In this case, I guess you could create an empty project with just a couple of dimension elements.

Maybe two could be the hand-made one and the API-generated one that work as expected.

Another could be the hand-made vertical one and the corresponding API-generated one that fails.

The macro could demonstrate how you go about creating them.

Would that work?

Thank you!

I wish you a wonderful weekend!

Best regards,

Jeremy

[FAIR59]

 You are creating dimensions and detail lines, so I think that you should be working on the sketchplane of the viewSection.

Plane geomPlane = doc.ActiveView.SketchPlane.GetPlane();

[FAIR59 · Accepted solution]

I looked better at your code and saw that you don't really use the geomPlane, so my previous comment is not valid.

I have found a method that will result in a "stable" dimension, (correct direction and value)

                XYZ point3 = new XYZ(417.8, 80.228, 46.8);
                XYZ point4 = new XYZ(417.8, 80.811, 46.3);

                Line geomLine3 = Line.CreateBound(point3, point4);
                Line dummyLine = Line.CreateBound(XYZ.Zero, XYZ.BasisY);
                using (Transaction tx = new Transaction(doc))
                {
                    tx.Start("tx");
                    DetailLine line3 = doc.Create.NewDetailCurve(viewSection, geomLine3) as DetailLine;
                    DetailLine dummy = doc.Create.NewDetailCurve(viewSection, dummyLine) as DetailLine;
                    ReferenceArray refArray = new ReferenceArray();
                    refArray.Append(dummy.GeometryCurve.Reference);
                    refArray.Append(line3.GeometryCurve.GetEndPointReference(0));
                    refArray.Append(line3.GeometryCurve.GetEndPointReference(1));
                    XYZ dimPoint1 = new XYZ(417.8, 80.118, 46.8);
                    XYZ dimPoint2 = new XYZ(417.8, 80.118, 46.3);
                    Line dimLine3 = Line.CreateBound(dimPoint1, dimPoint2);
                    Dimension dim = doc.Create.NewDimension(viewSection, dimLine3, refArray);

                    doc.Delete(dummy.Id);
                    tx.Commit();
                }

[Anonymous]

This solved the issue. I was able to adapt it to get the Y-dimension of the sloped line as well. Thank you for the solution.

[Moustafa_K]

@ FAIR59

Wow that was an interesting one. I wounder when you delete the dummy line, the sable reference of this line will remain exists permanently/temporary in the Database?, or it would be deleted later by (Audit, Purge, Compact in case of shared model)? I have not tested this, but some ideas came to my mind from what you sent. 

[jeremytammik]

Thank you very much for the solution and confirmation that it works.

I cleaned up, edited and published for future reference:

http://thebuildingcoder.typepad.com/blog/2017/01/vertical-dimensioning-and-revit-api-qas-research.ht...

Cheers,

Jeremy