PULL is Wacked
Hi,
Many thanks for posting this one. It does look like something is up here. The first thing I would check would be to take a look at the control points and see if there are snapping to an unexpected object in your model. If you change the Display Mode to Box mode (Alt+1 on Windows, Control+1 on Mac), you'll be able to see the control points of the surface. Have these snapped to an object in your model?
If you're able to share the f3d file, we'd be more than happy to take a look at this in detail. You can save the f3d file using the Export command, or if you right-click the model from the Data Panel, and select Share Public Link, and allow the item to be downloaded, I'll be able to access the file. You can post the model/link here, or email it to jake (dot) fowler (at) autodesk (dot) com.
Thanks!
Jake
Jake Fowler
Principal Experience Designer
Fusion 360
Autodesk
Accepted solution
Hi David,
Many thanks for the file, and for looking at the control points. You're right, something's definitely wrong here! Certainly something I've not seen before. I think the development team might need to look deeper into this one to figure out what's going on. Incidentally, this Pull will work ok if you choose to pull the control points to the eye, rather than the surface points.
One thing I did notice on the model is that there are a lot of star points around the eye area, and as a result, a lot of n-gons (i.e. non-4-sided-faces). You can see where the star points and n-gons are on your model by opening up the Repair Body tool inside Sculpt > Modify > Utilities, and selecting the body:
This is quite a high concentration of star points & n-gons, and I wouldn't be surprised if this was at least indirectly involved with the Pull problem. Did you intend for these to be star points? Many of these star points actually look like they would be better suited as T-points (since they encounter other edges at a T-shaped junction). Generally T-points are preferable to star points, as they're smoother and tend to result in more faces being 4-sided. We have a video here that explains what star points and T-points are (for more technical info, you could also check-out the T-Splines website).
In the Repair Body command, you can toggle star points to be T-points by clicking on them on the model. Given the number of these it will probably take some time; but this might help with your Pull issue, and as a side effect should also give you a smoother surface. The downside is that toggling these will change your smooth shape slightly (although this shape change could be significant if you're toggling lots of them), so you might need to do some work to adjust your smooth model back to the correct shape again.
Let me know if this does/doesn't work for you, or if anything's unclear.
Many thanks,
Jake
Jake Fowler
Principal Experience Designer
Fusion 360
Autodesk
Accepted solution
Thanks dunderhead & Kingson for chipping-in on this! And glad to hear that this eventually helped (although sorry that this resulted in more work for you). We’ll still look into what exactly is going on here, I don’t think it’s unreasonable to expect this to work as-is.
Totally appreciate the fact that this isn’t straightforward. Some concepts of T-Splines modelling are pretty unique & can take some practice to get a handle on. In general we try to give you the best topology automatically (i.e. usually in cases where T-points are possible, we’ll give you those by default). But there’s more we can do to make this more intuitive, and that’s an area we’re continuing to work on.
Do get in touch if you’re still encountering any issues with this.
Many thanks,
Jake
Jake Fowler
Principal Experience Designer
Fusion 360
Autodesk
David, from beginner to beginner, I thought I'd be able to help you: my understanding was something like a T point is allowed only where it makes sense, that is, as a refinement of a quad. The quad meshes are what most of your surfaces are made of. But there are exceptions, such as triangles and pentagons: those cannot be subdivided! So when you try to convert a star point to a T point you will only succeed if a quads results. If not, your T point is invalid and it will be marked in red.
But the reality is much more complex and I'm also at a loss! Sometimes you have to convert several star points before all of a sudden prior illegal T points become legal!! On the other hand, below is a situation where an single illegal T point is dozen of faces away from a conspiracy of three star point that seems to be controlling it. In fact, if you turn off any of the three star points marked by red arrows, by converting them to legal T points, then the illegal T point marked by a blue arrow also becomes legal!!!!!!
This action at a distance is against everything I had learned (?). It seems that for a larger model it might be quasi-impossible to understand forced boxification then?
Jake, you have been very helpful with other questions, I hope you have an answer for this one! I have looked in the Tspline 3 manual, I have looked at T-splines and T-NURCCs but I still don't get it. In particular, an important implication (?) is that the automated repair offered by the "repair body" operation is then essentially misguided: it'll sometimes insist on converting illegal T points to star points --- instead of further simplying the model by converting star points to T points.
Accepted solution
I'll give it a shot! Error T-Points are a fairly tricky & technical one to explain, so apologies in advance if this isn't very clear...
NURBS geometry (on which T-Splines is partially based) has a concept called 'knots' (sometimes referred to as 'spans'). NURBS curves & surfaces work by effectively tying a bunch of mathematically simple curves/surfaces together - using these knots - in order to form complex splines that couldn't easily be defined with a simple equation. NURBS curves & surfaces all have a hidden property called a knot vector, which is used behind-the-scenes to define the spacings between these knots. (It might be worth Googling "NURBS knots"/"NURBS knot vectors" for a fuller explanation; a quick search brought up this technical paper, which gives quite a good introduction).
In T-Splines, you can think of each chain of edges as a knot in the T-Splines surface. The values for the spaces between the knots are actually arbitrary (it's the relative proportions between them that's important, not the actually values). So for this box, let's say the spacing between each pair of knots is 1 (here I'm just showing the knot spacings between two edge chains flowing in one direction; but you have the same thing between all pairs of edges in all directions):
If use Insert Edge to insert a single edge at the top of the box, it's going to add two new T-points, which effectively 'splits' the knot spacing here:
If I inserted this edge exactly halfway, the spacing between the new edge and neighbouring edges will be 0.5 on each side:
The numbers all add up nicely here, and I end up with two valid T-points.
A red T-point occurs when a split is created in a way that doesn't add-up nicely (i.e. where the topology doesn't allow for a 'sensible' knot spacing values). For example, I'll add an edge, but this time I'll use the Insert Point tool, and insert an edge from the midpoint on one side of the face to a corner on the opposite side (you can already see that this has given me a boxy result; '3' just indicates a 3-sided face here):
The reason that this T-point is 'bad' is that it has introduced an ambiguous knot spacing (at the yellow segment here):
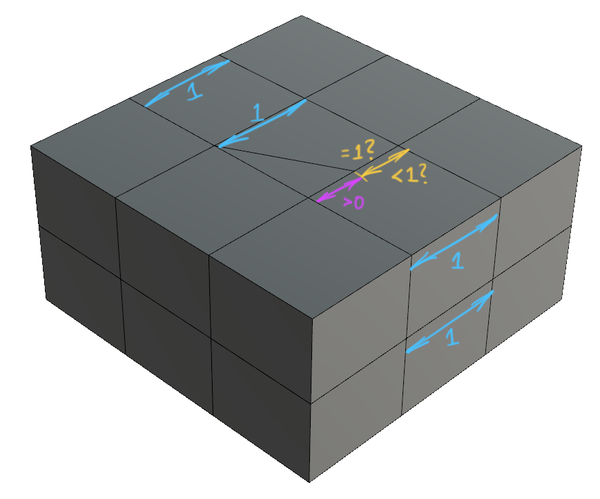
Travelling along the highlighted chain of faces, the knot spacings from upper-left downwards dictate that the yellow segment should have a knot spacing =1. But travelling up from the bottom-right of the image, the yellow segment and purple segment must add up to 1. If the purple segment has a knot spacing of >0 (which really it needs to), the yellow segment must have a knot spacing of <1. We have a conflict on what the knot spacing of this yellow segment should be, and this is what causes this T-point to be erroneous, and prevents us for getting a legal smooth surface.
If this T-point it swapped for a star point, the 4-sided face with the T-point just becomes a 5-sided face:
N-gons (i.e. non-4-sided faces) are not really concerned with how adjacent knot vectors add-up (this 'adding-up' only really happens when you have a T-point entering a 4-sided face). Since there are no T-points here, we could just make all the spacings 1 and everything works out nicely again:
So... with these 'knot spacings' in mind, you typically get red T-points when you have face loops looping back on themselves in a way that causes one of these ambiguous situations. I'm guessing that dunderhead's example might exhibit something like this; try following the faces around the model starting at that T-point.
Repair Body will tend to convert these to star points, because this will nearly always resolve a situation like this. At the moment the main aim of Repair Body is to fix errors on the model, rather than optimise the quality of an already-legal model. But you do raise an interesting point - perhaps more intelligence could be added to this tool. I'll follow up with the team here to see if there might be any smart way to replace 'unnecessary' star points with nicer T-points (this might not be straghtforward, since star points usually have mulitple potential T-point solutions... but worth looking into!).
Does that help at all? If anything here wasn't clear, let me know and I'll do my best to clarify.
BTW, if you're searching the T-Splines website, it's probably worth searching the term 'seashells', as this is what error T-points are referred to in T-Splines for Rhino (you can reproduce this effect with a simple 2D seashell-like arrangement of faces).
Thanks,
Jake
Jake Fowler
Principal Experience Designer
Fusion 360
Autodesk
Jake, thank you for taking up this challenge, your example is most helpful! Drawings are excellent, hope you can find a place for this explanation somewhere in the offical documentation.
After I played with it in Fusion 360 I see that it all works exactly as you explained. If you remove the bottom of the box then there is no problem having a diagonal edge: there is no cycle. On the other hand, if you just add another diagonal edge, abolishing all T points, but adding another star point, then again there will be no problem, there will be no confusion about what constitutes a quadrangle, which is what I believe is at the heart of the knot labeling issue.
I think I found another issue, which could be quite bothersome. I hope you can just confirm my understanding.
In the current UI, you can click on a point several times in the repair body mode to cycle through various labelings. Below I click repeatedly on the point, near the center of the picture, which alternates between being a star point and yellow and red T points:
At least here one of the configurations is all yellow (which means that the T-spline is rendered in smooth mode automatically, but I cheated when I made the animation to not have the distraction of the changing surface)!
Now for the issue: it turns out that finding the smooth solution was by luck only! By clicking on some of the other nearby T-points (in a particular way), without changing them to star points, it becomes impossible to render the face in smooth mode by simply toggling the same point near the center of the picture as before.
In other words, it seems as if it is perfectly possible to have a T spline that is legal but cannot be rendered in smooth mode without blind and manual probing at various T points! The decision by Fusion 360 whether a "form" is smooth or not is itself then essentially random, at least for structures with lots of T points, is that right?
The automated repair is unhelpful in this particular example: it will make tons of star points, that is one way to reduce the exponential solution space.
I think there is an underlying combinatorial problem here, probably involving a 2-coloring of the edges under some very simple constraints, which entail a binary decision for each T-point. Is that true?