Is there any Lisp routine to align a particular line segment of a given block on

[SanjoyNath]

Dear Experts,

We are working with some blocks which looks like wedges (Simple Right Angled Triangles) . All blocks are looking similar (copied entities)  . We want to generate all possible alignments (4 types of symmetry possible per alignment) 

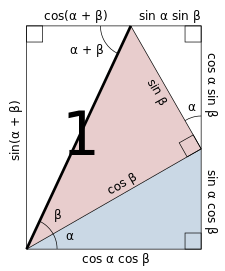
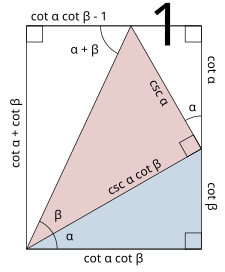
Here in the picture below i have done the manual work of triangle where Hypotenuse of second Right Angled Triangle is aligned with Perpendicular of First Right Angled Triangle(Scaled to fit) . If we chose different sides of line segments from Right Angled Triangles , then we get different kinds of options of alignments. Some of these are not intended and some of these are intended for our drafting needs.

I need exhaustive list of pictures possible due to these alignments (Wrong geometry or right geometry both to include)  and need separate arrangements pictures (on the drawing) due to different types of Alignments points chosen . Here only Sin(Θ) is used and only one x is there which means only one  * operator is done so , only 4^1 arrangement to generate . If such multiplication increases , then possible pictures will form like large possible options which is tough to draw manually on Autocad

I have made triangle shaped blocks. i have put Hypotenuse in Hypotenuse layer , Base in the Base layer and the Perpendicular in perpendicular layer

Now , if i type command GT it will ask for option(sub commands) like <HP>,<HB>,<BP>,<PH>,<PB> ,<BH> ...

example

<HP> means i want to align and scale to fit Hypotenuse of second similar block on Perpendicular of First Block with all possible pictorial options

<HB> means i want to align and scale to fit Hypotenuse of second similar block on Base of First Block with all possible pictorial options

<BP> means i want to align and scale to fit Base of second similar block on Perpendicular of First Block with all possible pictorial options

<PB> means i want to align and scale to fit Perpendicular of second similar block on Base of First Block with all possible pictorial options

<PH> means i want to align and scale to fit Perpendicular of second similar block on Hypotenuse of First Block with all possible pictorial options

<BH> means i want to align and scale to fit Base of second similar block on Hypotenuse of First Block with all possible pictorial options

The picture here shows the algorithm which i have used in c#

Detail logic is written here

https://github.com/SanjoyNath/GeometrifyingTrigonometry/wiki

More clue is here

Theorem(Geometrifying Trigonometry)For k numbers of * found in any sub trigonometric expression (tha...

if there are n1 numbers of multiplication in given Trigonometric Expression and n2 numbers of divisions there then

k=n1+n2

if there are total k numbers of multiplications and division in a Trigonometric expression then 

[(k+1)!] x (4^k)  numbers of (maximum) pictorial arrangements possible which is very tough to draw manually.I am writing the framework in c#  here  for CAD which needs closing and reopening of CAD to update plugins everytime which is tedious.So i need lisp for this to avoid frequent closing and reopening CAD

[CodeDing]

@SanjoyNath,

It's quite hard for me to understand what you're question / desired outcome is.

Anyways, I created a LISP to duplicate your Copy/Rotate/Scale option.

I noted where others could add a (grread) function that would accept your "\" and "/" operators for mirroring as desired.

Maybe I'll get some time in the future to expand on that.

The (GetAlignment) function can be recurring (called from within itself).. this can allow you to to call it X^n times. I think you mention this ability? I'm not sure.

For further assistance from others, you might need to make it more clear as to what you need answered/assisted with. I had a hard time following, so maybe others did also.

ATTACHED:

- .lsp that can be called with command "GT" (see notes in lisp for ASSUMPTIONS)

- .dwg with 2 blocks (triangle & triangle2)

***one block made from lines, the other from polylines

***there are 6 examples from each block showing your 6 outcomes (HP/HB/BP/BH/PB/PH)

Best,

~DD

[SanjoyNath]

Thank you very much @CodeDing

You have understood this very well and the thing is working fine only with one option

We need to get copy of all these for four different options can form for each of these HP , HB , PH , PB , BH etc...

For each of these commands there needs generation of four different pictures recursively.

Lisp looks tough for me.You are great

To the best i could understand is to call CopyAlign  functions for each conditions four times with copied arrangement

(cond
((eq "HP" ans) (setq entNew (CopyAlign entOrig (car lst) (cadr lst) ptBase)))      This will give all pictures of [Sin(Θ)]^2
((eq "HB" ans) (setq entNew (CopyAlign entOrig (car lst) (caddr lst) ptBase)))   This will give all pictures of [Sec(Θ)]^2
((eq "BP" ans) (setq entNew (CopyAlign entOrig (caddr lst) (cadr lst) ptBase))) This will give all pictures of [Tan(Θ)]^2
((eq "BH" ans) (setq entNew (CopyAlign entOrig (caddr lst) (car lst) ptBase))) This will give all pictures of [Cos(Θ)]^2
((eq "PB" ans) (setq entNew (CopyAlign entOrig (cadr lst) (caddr lst) ptBase))) This will give all pictures of [Cot(Θ)]^2
((eq "PH" ans) (setq entNew (CopyAlign entOrig (cadr lst) (car lst) ptBase)))This will give all pictures of [Cosec(Θ)]^2
);cond

CodDing_has_done_this_GT command from codding in the autodesk forum for SanjoyNath(C)GeometrifyingTrigonometry_3.1.2019.png

@CodeDing Thank you again.Please see this picture as above.We need these options in one go with GT command

(for each options there needs four pictures)

Please see this picture also

 @CodeDing CODDING of autodesk has given the lisp to generate single option for SanjoyNath(C)GeometrifyingTrigonometry(C)AlgebraicStructures

 Fantastic thing will happen if we can get all these pictures in one go for typing GT then option.If we get all these possible pictures then we can put less stress on Intuitive hardworks for visualizations

Please see this also

https://forums.autodesk.com/t5/autocad-forum/how-can-i-get-all-possible-geometric-shapes-from-given/...

[CodeDing · Accepted solution]

@SanjoyNath,

 Thank you for clarifying.

The updated .lsp can now accomplish all 4 views for the block (s). See attached for .lsp and .dwg.

^^^"HP" arrangement after block selection

^^^Works for blocks with Polylines & Lines

EDIT:

After more testing, I should note that this routine will not correctly interpret a Scaled or Rotated block.

Best,

~DD

[SanjoyNath]

Dear @CodeDing

@CodeDing

This is fantastic and quite Amazing that you have done this.Obviously i need to explain this for you specially because it is quite natural to come to mind that why we are trying to convert existing Trigonometric equations into another notations.Computers cannot do recursive calculations until it is converted to String Formats.Computers can do work with syntax checking systems.So Regular Expressions are necessary to make any problems computable.Due to that reason we had to model the whole Trigonometric expressions into Stringology forms where we can implement recursion

RECURSION FRACTAL is the key here.The moment this lisp(as you have fantasticly developed) will recursively generate all possible pictures(NOT INFINITE) it is FINITE (            [ k+1]!  x  (4^k)  for k numbers of multiplications or divisions present in the (Any) given Trigonometric expressions) proof is there in 

https://geometrifyingtrigonometry.quora.com/Theorem-Geometrifying-Trigonometry-For-k-numbers-of-foun...

So we need to get all these options.

Step 1  to generate a triangle block for the Θ (choicing within 0 to 45 normally)

Step 2 to  Convert all Sin(Θ) as HP , All Cos(Θ) as HB , Convert all Tan(Θ) as BP as given in the links. This is stringology

Step 3 to do all possible necessary calculations we have given the complete algorithms there in github (I am writing c# and excel vba for that) LISP looks tough for me . Thank you Again @CodeDing   . Fractal and recursions will help us getting all possible options there(Autocad can handle more infinite options than other softwares)

Thanks And Regards

Sanjoy Nath

http://www.structuresonline.net/

Endeavour for Mission Zero Editing

https://github.com/S...igonometry/wiki   

 [Computational model and Computable Algebraic Structure Engine(API on the making) of Trigonometry to keep line segments on Drawings Or Model at right place after Trigonometric calculations]

1.Theorem(Geometrifying Trigonometry)For k numbers of * found in any sub trigonometric expression (tha...

2.Geometrifying Trigonometry is Different From Vector Algebra

3.Corollary:Geometrifying Trigonometry: Cos(Θ) x Sin(Θ)=Sin(Θ) x Cos (Θ) has 25% Chance to become equa...[NON COMMUTATIVE ACTUALLY ,SO USING OF TRIGONOMETRY CAUSES AMBIGUITY SO DRAWING OBJECTS JUMPS AROUND]

3+.    37  IMPORTANT Line Segments and 10 Points Identified to Symbol set Σ of Geometrifying Trigonometric©... [ EVERY TRIGONOMETRIC EXPRESSION SIGNIFIES SOME IMPORTANT LINES ON 2D DRAWINGS TO ALIGN]

3++. Right Angled Triangle is simplest Locked Set in Geometrifying Trigonometry  [ Theoretically looking similar does not mean Geometrically Similar  ](*,)          ]

6.The Forgotten Line Segments in Trigonometry

7.Mission Zero Editing Stumbles in Geometry where Vectors cannot answer Trigonometric Identities     Automated Symbolic formulation of operations and formations due to operations on GT Strings in Geome...

8.Theorem 10: Geometrifying Trigonometry :There are 6 Types of Equality in Geometrifying Trigonometry....

9.Theorem 7:Geometrifying Trigonometry: Every Compound Douplet String of Geometrifying Trigonometry Do...

10.Operators , Their actions and Interpretations on GT String

11.Theorem (Geometrifying Trigonometry©) Conformal Transformation holds before and after * operation

[SanjoyNath]

Dear @CodeDing

Thanking you again.

Please see the pictures i could prepare very fast (I think world has never seen these before)

These are the pictures for Squared data on Trigonometric expression where single * operation is done.So your lambda functions called rightly and prepared these by superimposing Line segments on line segments

Now challenge is to call these lambda recursively when there are more than one * operations are there.

Suppose if we want to prove these 

https://en.wikipedia.org/wiki/List_of_trigonometric_identities

Suppose if we want to prove these identities pictorially @CodeDing , Lisp need to prepare these automatically without using human intuitions. We want to make program which will draw these pictures from the formula writen like this

    or

or

Autocad will draw ( @CodeDing@ CodeDing Lisp will draw these automatically through the use of GeometrifyingTrigonometry(C) recursions logic)

Then for next stages

We wish that we will write Trigonometric Expressions like these and Lisp will draw all proof pictures from there.

Autocad will become must use software for mathematicians also

Sin^2 (Θ) + Cos ^2 (Θ) = 1 proved now

https://geometrifyingtrigonometry.quora.com/Interpretation-of-Pythagoras-Theorem-in-Geometrifying-Tr...

Thank You Again @CodeDing

Ok

For Simplicity we can start drawing all pictures for these first

[SanjoyNath]

Again @CodeDing

Please see how much you have helped to prepare all these pictures.If you add the recursion , then Autocad will become mathematical proof engine

Please see 16 pictures of Cos Cubed Theta

There are two multiplications in Cos Cubed Theta so 2 times * operations done so (3!/3!) x (4^2) = 16 pictures formed

Thank you very much

Please see the attached Dwg file here

[CodeDing · Accepted solution]

@SanjoyNath,

Attached is GT2.lsp. I started over to incorporate no "command" calls while drawing.

I no longer have time to keep working on this. I have completed it to the best of my current ability.

Notes:

- call with "GT" command

- Triangles are created with lines instead of creating/copying blocks

- BE CAREFUL... doing 5, 6, or 7 recursions "Layers" is very taxing on AutoCAD! Anything more might need a super computer to draw Lol.

...I am not going to guarantee the accuracy of this lisp or its output. I wish I could but, like I said, I have no more time to keep working on this.

Ultimately, this may be more efficient / faster if decoded and created to run with .NET... but idk.

The output can look pretty cool though. I wish you the best in your advancement with this!

Image of 5 "Layer" output.

Best,

~DD

[SanjoyNath]

Fantastic @CodeDing

Thank you very much.This is fantastic