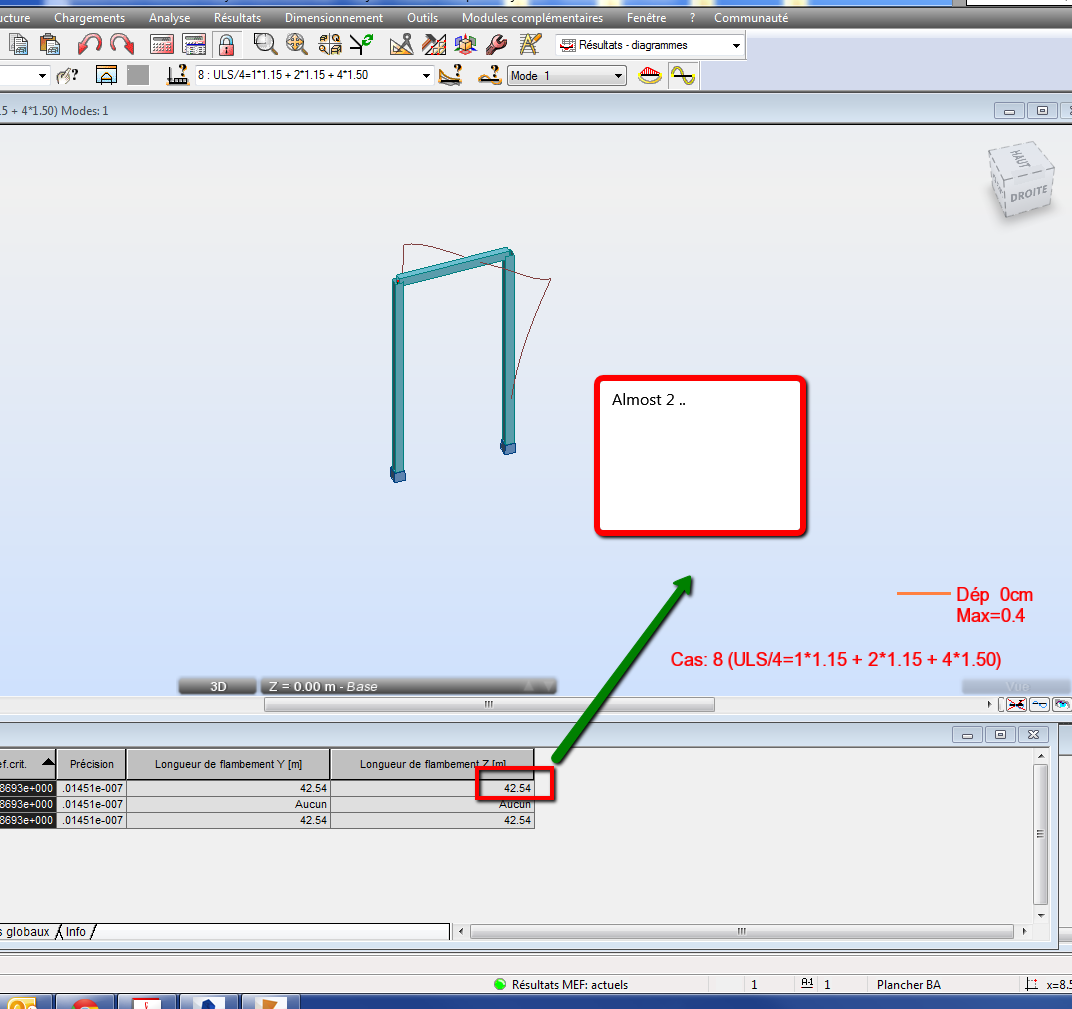
To follow on a bit this topic.
I read some things about the buckling analysis (general buckling). From this, I now understand that one has not to mix mode corresponding to a local buckling (in this case the analysis gives the same results than the when unsing the checkings member module) with one corresponding to global mode for the whole structure.
What is still hard to understand :
Basically the analysis consists of a matrix problem with eigen values:
1) KF=D is the problem and Robot diagonalize the matrix K and return eigen vectors and critical forces
2) Step 1) is repeated with K' (updated matrix) and D' = x time D till the problem return a K' to low (loss of rigidity), but what is the criteria to consider there is a too big loss of rigidity and then this is a buckling mode?
3) it calculates F crit which is Fat the first step in each member multiply by x (final amplification factor) for all bars, case etc ...
4) With euler's formula, it gives "theoretical" buckling lenght for each member
Second question is : physically, these results/analysis cannot be interpretated as the buckling of the weakest member for a particuliar load case for a particuliar structure? It is a global loss of rigidity and not necesseraly due to the loss of one sole member?
Last question (I thnik the answer is trivial but please confirm): If the analysis is done on a load case with several forces in several directions : all the forces are multiplied by a unique factor ... ? not only the forces which clearly destabilize the structure (horizontal for example) -> here come the engineer to find the appropriate load case / comb to analyse and find the smallest critical coefficient for all the studied situations ?
Thanks a lot for your answers.
TS